A computer algebra system, or CAS, is a program that allows the user to enter mathematical expressions and perform calculations on them. For example, a general computer algebra system can help with the following tasks:

• Solving an equation for a variable
• Factoring a polynomial
• Taking an integral with respect to a variable
• Taking the derivative with respect to a variable
• Plotting a function, in 2D or 3D space
• Simplifying an expression
• Transforming expressions to different forms

The language

Some computer algebra systems implement their own languages. These languages tend to be symbolic and perfectly happy working with symbols/variables that are undefined. After all, most equations have plenty of undefined variables in them. These symbolic languages tend to not have much of a distinction between code and data. It’s quite common to pass expressions as arguments to functions when the expression itself is nothing more than a piece of code that has unevaluated symbols within it.

In[1]:= a = 1; b = 2;

In[3]:= a + b

Out[3]= 3

In[4]:= a + b + c

Out[4]= 3 + c

In[5]:= Integrate[a + b + c, c]

Out[5]= 3 c + c^2/2

Wait, what happened here? Was the language alright with c being undefined when we added that symbol to the mix? Yes it was. In fact, we can even pass this partially-undefined into an integration function to integrate it with respect to c. This language above, by the way, is the Mathematica language. The last line effectively computes the indefinite integral:

We could do something similar with Sympy, another computer algebra system, but this framework piggybacks on Python, which does not allow for undefined symbols. Sympy uses a solution involving declaring in advance “undefined” variables, allowing them to have a definition according to the Python runtime, but the manipulation functions within Sympy will understand that these objects are actually free variables.

Symbolic vs. Numeric

Image source

Now if we look at the list of CAS operations above, it’s true that many can be done without symbolic calculation in a numeric way. In fact this is a big criticism of symbolic calculation for many purposes. When working on pure math, it is indeed important to work with exact expressions, but many forms of applied math are only interested in the numeric result. Many well behaved derivatives and integrals can be found numerically through numerical differentiation and numerical integration. There are even specialized methods for finding solutions of differential equations like Runge-Kutta. These methods all return approximate numeric results. They work great for simulations and computer graphics, but some use cases require exact symbolic answers to questions. Other use cases involve equations that are unstable under these numerical methods, and thus we must find a symbolic solution. This is where computer algebra systems shine, in addition to simply allowing students and researchers explore mathematical concepts without wasting time on redundant tasks.

Internals of expressions

There’s no right way to build a CAS, but the system I’m most familiar with is Mathematica. I’ve implemented a large chunk of the language in a BSD-licensed project called Expreduce. For the rest of this post I’ll talk specifically about how Mathematica/Expreduce works to help readers become more familiar with CAS concepts.

Expressions in Mathematica and Expreduce for a tree of tagged lists. Here is an example of $(x+y)^2$:

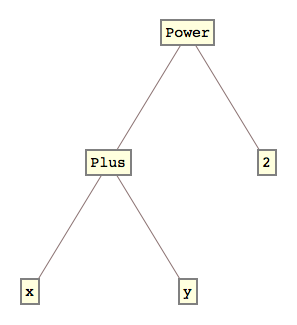
And if we wrap an Expand[] function around this expression, the evaluator runs a few replacement rules and eventually ends up with this expanded expression of $x^2+2 x y+y^2$:

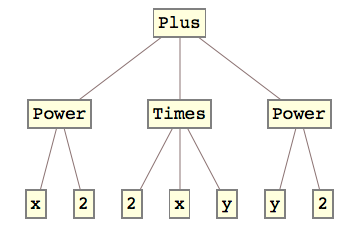
Database of rewrite rules

Mathematica, Expreduce, and many other computer algebra systems have a massive database of rewrite rules that are either applied automatically in certain contexts or during explicit function calls. For example, take this excerpt from the Expreduce source code:

Sin::usage = "`Sin[x]` is the sine of `x`.";
Sin[0] := 0;
Sin[-x_] := -Sin[x];
Sin[p_Plus] := -Sin[-p] /; (MatchQ[p[[1]], -_] || p[[1]] < 0);
Sin[x_Integer?Negative] := -Sin[-x];

...

Cos::usage = "`Cos[x]` is the cosine of `x`.";
Cos[0] := 1;
Cos[Pi] := -1;
Cos[n_Integer?EvenQ*Pi] := 1;
Cos[n_Integer?OddQ*Pi] := -1;

The syntax here can be quite dense, but it sticks quite closely to traditional mathematical notation. The evaluator checks these definitions every time it encounters an unevaluated instance of a Sin[] or Cos[] expression. If it encounters a $\cos$ expression with an input that evaluates to an even multiple of $\pi$, then it will replace it with the integer 1.

These rules don’t need to be limited to the explicit “functions” we are used to in normal programming languages. We can and do change the behavior of addition through definitions like these. We can say that subtracting like expressions cancels them out. We can say that two like expressions can be replaced with two times that expression.

Commutative and associative matching

Perhaps the most important aspect of a computer algebra system is the understanding of commutative and associative operations. Mathematica and Expreduce understand these commutativity and associativity through Orderless and Flat tags applied to symbols, respectively.

For example, the Plus operation is both Orderless and Flat:

In[23]:= Attributes[Plus]

Out[23]= {Flat, Listable, NumericFunction, OneIdentity, Orderless, Protected}

This has a number of very important implications for pattern matching. One important implication through the Orderless attribute is that the evaluator automatically sorts addition terms into a canonical order as soon as possible. This means that when checking for like forms to combine,we really only need to check terms against their neighbors. Computer algebra is filled with nasty traps of $n!$ complexity unless we use tricks like this.

These attributes help us with rule definition. Let’s say we want to define the product rule in calculus:

We need to think about how we implement this in practice. What if we have more than two expressions multiplied together, such as $a \cdot b \cdot c$? Do we need to take care of the recursion for this ourself? It turns out that because the evaluator understands that Times is both commutative and associative, we can use this simple definition:

D[a_*b_,x_] := D[a,x]*b + a*D[b,x]

Notice how this is essentially a verbatim copy of the definition we would see in a math text. And it works! This is the definition for the product rule in Expreduce right now.

Conclusion

Trying a computer algebra system for the first time might feel like magic in the sense that we know there are a lot of strange computations going on under the hood but we don’t know exactly what they are. I built Expreduce because I wanted to understand that magic, and in the process I found that computer algebra involved very neat tricks and algorithms that I hope to share in future posts.